Tournament Structure 101
If you are new to tournaments, this is for you 💁🏻♂️
Knowledge is Power
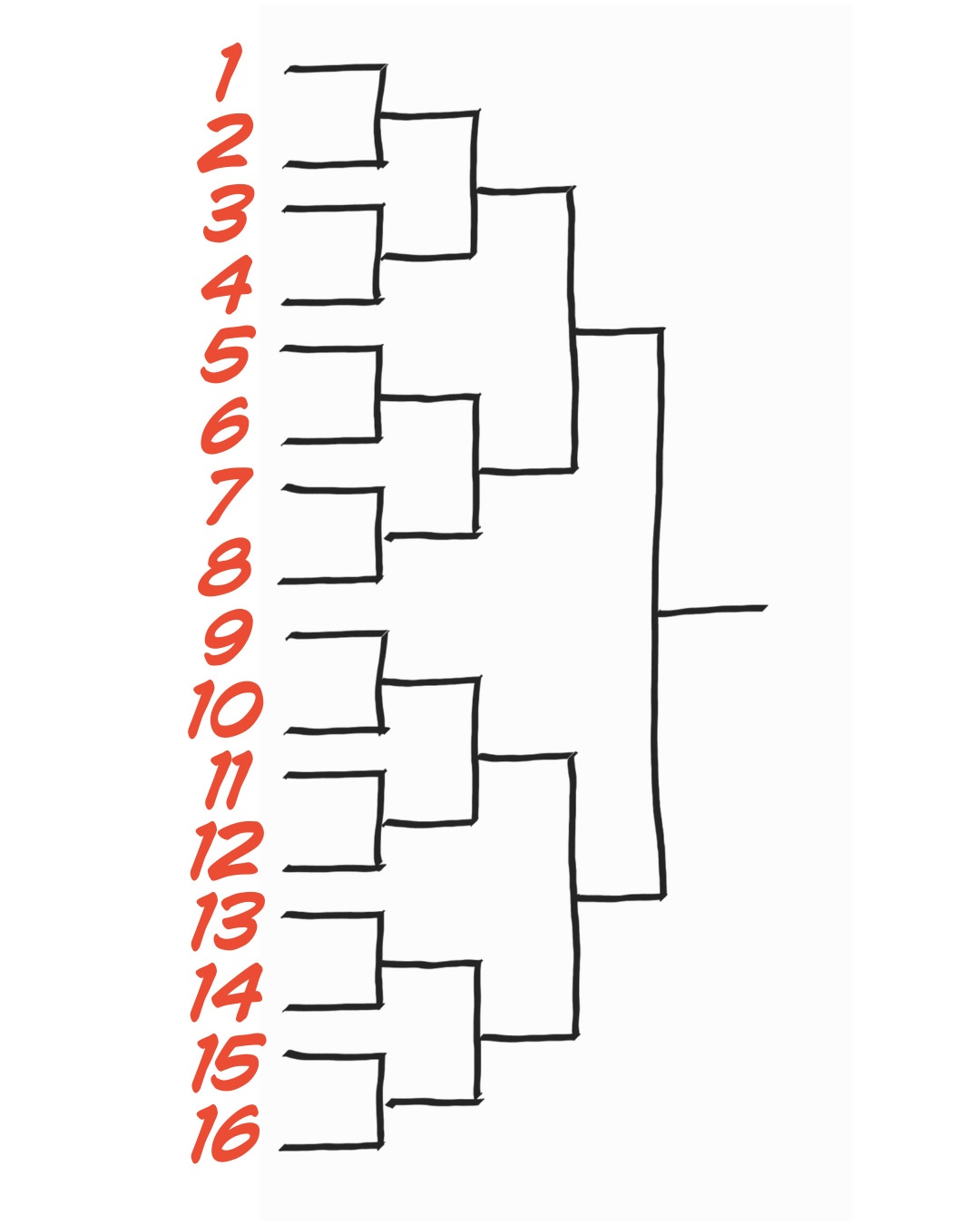
In many badminton tournaments, the main draw consists of elimination brackets. However, it is easiest to understand if we start from the end.
In a final, a match is played between 2 players or teams. For simplicity, we will use “teams” from now on. This should be obvious, as the winner of the final is the tournament champion.
What about the previous round: the semi-finals ?
How many teams are there in semi-finals? If the winner of each match competes in the final, then each finalist must have won their respective match. We have two winners, and two losers (i.e. semi-finalists), which means we have four teams in the semi-finals. That also means three matches are played (two semis, one final).
Let’s continue with the quarter-finals .
If we have two in the finals and four in the semi-finals, then we must have eight in the quarter-finals. How many do we have in the Round of 16 (hint: it rhymes with “ixteen”).
How about the Round of 32 or Round of 64? We can go further than that, but tournaments usually cap at 64 teams because that’s already 63 main draw matches! Let’s do the math for a perfect 64 draw:
1 Final + 2 Semi-finals + 4 Quarter-finals +
8 Round of Sixteen’s + 16 Round of Thirty-two’s + 32 Round of Sixty-four’s.
Let’s group them together for easy math:
(32 + 8) + (16 + 4) + (2 + 1) = 40 + 20 + 3 = 63 matches.
It’s easier to reference R64, R32, R16, QF, SF, or F instead of the ambiguous “Round 1” or “Round 2”, because “Round 1” can mean different things based on the draw size. If there are 17 players in a draw, what is "Round 1"?
It's R32 (round of 32), because two unfortunate players will have to play for their spot to belong in R16. Technically, R16 in a 17-team draw is "Round 2". But if we only have 16 players, then "Round 1" is R16. That's why using "Round 1" or "Round 2" is ambiguous, even though it's used on TournamentSoftware, where the majority of badminton tournaments is hosted on.
Other Formats
ROUND ROBIN
Round Robins are often used when there are small team sizes in a draw. This means that each team will play all other teams in the pool. For example, if there are three teams, then each team will play two matches (e.g. Team A plays Teams B & C). However, total matches grow non-linearly with each additional team:
3 teams = 3 total matches
4 teams = 6 total matches
5 teams = ?
Let's see if you can figure this out with the help of The Quintessential Quintuplets. If you don't know what I'm talking about, don't worry about it. 😅
This follows the formula of:
where n is the number of teams, and 2 represents the number of teams per match. Yes, we can discuss factorials and binomial coefficients, but that is not necessary for tournament structure, unless you’re doing tournament organization.
However, we can also use intuition and look at things visually:
Notice that this is a visualization of the formula. Given our formula, we can multiply the n with (n - 1) to get (n² - n). Using the Quintuplets (i.e. 5), we get a 5 x 5 grid = 25 squares. We then subtract the match up where each Quintuplet would be facing herself (i.e. 5), which lines up with the first part of the formula:
n² - n = 5² - 5 = 25 - 5 = 20
The last part is to divide 20 by 2, which gives us 10 matches.
Using the formula, how many matches would we have with 6 teams?
Visually, we can see another pattern forming. It looks like there’s a 1 + 2 + 3 + 4 + … pattern, and yes, if we add everything together (up to 5), we would get 15 matches for 6 teams. It makes sense intuitively too. When we add another player, that player has to play everyone once on top of the previous matches.
If you have the time for matches, then round robin works well. However, sometimes we may have small draws for some events, and large draws for others. If we want to minimize matches so that everyone can get the chance to play, what else can we do?
POOL PLAY
This is a combination of round robins and elimination draws. Let's say we have six teams. Instead of playing a 15 match round robin (too many!), or elimination draw of 5-8 matches depending on consolations (maybe too few!), we can try a style called Round Robin to Elimination (RR2E). With six teams, we have two pools of three teams, and then they go into an elimination draw. There's some flexibility here, because we can have teams play teams in the other pool based on their placement (i.e. top in pool A plays top in pool B for first place, second in pool A plays second in pool B for third place, etc.).
How many matches would there be for six teams, using this format?
2 pools x 3-team Round Robin = 2 pools x 3 matches per pool = 6 matches
The elimination draw will have a minimum of one match (i.e. finals). A 3/4 playoff can be played, but I wouldn't recommend it if other events don't have one. Each team is still guaranteed two matches from the round robin, and the finalists get a bonus match.
6 matches (pool play) + 1 final match (elimination) = 7 matches
In the case of 5 teams, RR2E can still work well with a 3/4 playoff. Pool A will only have two teams (because first seed will have less matches), and Pool B has three. Here's the math:
1 match in Pool A + 3 matches in Pool B = 4 matches
Top two teams come out, and play for first and third place respectively = 2 matches
With six total matches, everyone still gets at least two matches, and you can save four matches from being played if time is a constraint.
Congratulations, you have now completed Tournament Structure 101!
